이 포스트는 K-MOOC 숙명여대 여인권 교수님의 통계학의 이해 Ⅰ 강의를 기반으로 작성되었습니다.
이번 시간에는 통계량의 확률분포인 표집분포와 표본평균의 통계적 성질에 대해 알아보고자 한다.
표집분포 (sampling distribution)
표집분포란 지난 시간에 배운 통계량의 확률분포이다. 통계량이란 측정가능한 확률표본의 함수로 표본평균, 표본분산, 극한값, 범위, 순위(Xi 크기 순서) 등이 있다. 이러한 통계량은 우리가 주로 관심을 가지는 모수와 연관되어 있기 때문에 이 통계량이 어떤 통계적 성질을 알고 있는지 파악하는 것은 중요하다.
ex) 어떤 확률분포 두 확률표본을 추출한 경우, 두 표본평균의 분포는?

위의 예시를 일반화한 표본평균의 기댓값, 분산 등을 구하면 다음과 같다.
그리고 이러한 통계량의 표준편차는 표준오차라고 하며 σ/√n으로 계산된다.

그렇다면 이러한 표본평균의 분포는 어떻게 될까?
먼저, 모집단이 정규분포인 경우를 살펴보자. 지난 정규분포에 대해 배웠을 때, 정규분포의 선형결합도 정규분포라는 사실을 알 수 있었다. 이를 이용하여 정규분포 표본평균의 분포를 구하면 마찬가지로 정규분포가 나오게 되며, 평균은 동일하고 표준편차는 위에서 구한 표준오차와 동일하게 나오게 된다.

그리고 표준화를 하는 경우, 마찬가지로 N(0,1)인 분포가 나오게 되며 표준화 식은 아래와 같다. (자주 나오는 중요한 부분이니 잘 기억해두도록 하자.)

다른 분포를 나타내는 것 중 대표적인 것은 정규분포를 포함하고 있는 지수족(exponential family)이 있다.
여기에서는 두 확률변수 X1, X2를 더했을 때 나타나지는 분포에 대해 나타내고 있다.
이항분포, 포아송분포, 음이항분포는 이전에 다룬 적이 있는데, 뒤에서 배우게 될 감마분포에 대해 간단히 설명하자면 모양을 나타내는 모수 β와 척도를 나타내는 모수 α로 나타나지는 것이다. 그리고 이 감마분포의 특수한 형태로 지수분포, 카이제곱분포 등이 있다.
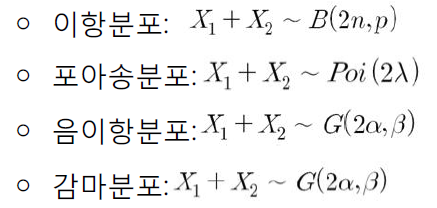
아래에 나타나져 있지 않은 다른 분포들의 경우에는 어렵지만 직접 유도 또는 근사분포를 유도하거나 몬테카를로(Monte Carlo) 모의실험을 통해 표집분포를 추정하고 있다.
몬테카를로(Monte Carlo) 모의실험
X=X1+...+Xk라면 해당 분포에서 표본을 k개만큼 뽑고 모두 더해 x를 구하는 것을 정해진 횟수만큼 반복하는 것이다. 이는 통계학에서 중요하게 사용되며, 앞으로 발전될 통계학의 방향성을 나타내고 있다.
ex) Xi ~ Poi(1)일 때 X=X1+...+X15의 분포 : X~Poi(15)
이를 통해 몬테카를로 모의실험을 하면 다음과 같다. 우선 포아송분포의 λ가 1인 집단에서 표본 15개를 뽑는다. 그리고 그걸 합해서 x 하나를 구한다. 이런 식으로 10만번 반복해서 이의 형태를 보는 것이다.
예를 들어, 표에서 x=3인 경우 x가 3보다 적거나 같은 것이 몇개나 있는지 그 비율을 보는 것이며, 작은 값과 큰 값에서는 거의 정확한 확률과 모의실험결과가 일치하는 것을 볼 수 있다. 여기에서 허용오차란, 실제 값과 벗어날 수 있는 영역이 어느정도 되는지를 나타낸 것이다. (뒤에서 다시 설명할 예정)

'MATH & STATS > STATISTICS' 카테고리의 다른 글
| [통계학] 12-3. 표본분표 - 이항분포의 정규근사 (0) | 2020.03.11 |
|---|---|
| [통계학] 12-2. 표집분포 - 중심극한정리 (1) | 2020.03.11 |
| [통계학] 11-3. 정규분포 - 확률표본과 통계량 (0) | 2020.03.10 |
| [통계학] 11-2. 정규분포 - 정규분포의 성질 (0) | 2020.03.10 |
| [통계학] 11-1. 정규분포 - 정규분포와 확률계산 (0) | 2020.03.10 |



