이 포스트는 K-MOOC 숙명여대 여인권 교수님의 통계학의 이해 Ⅰ 강의를 기반으로 작성되었습니다.
이번에는 이항분포의 확장된 형태인 다항분포에 대해 알아보고자 한다.
이전에 범주화된 자료를 정리하는 도수분포표를 배울 때, 도수와 상대도수에 대해 배운 적이 있다. (링크 참고)
해당 범주에 속해 있는 자료의 비율을 나타내는 상대도수는 표본을 계속 뽑으면 해당 범주가 모집단에서 차지하는 비율, 즉 확률로 수렴하게 된다.
다항분포 (Multinomial Distribution)
지난번에 다룬 이항분포의 경우 발생 가능한 결과가 2가지(ex: 성공과 실패)만 나왔다. 이제는 발생 가능한 결과가 2가지 이상인 경우를 살펴보고자 한다.
다항분포란, 각 시행에서 발생 가능한 결과가 k가지로, 각 독립적인 시행에서 i번째 결과 확률은 p_i로 고정시키는 것을 말한다. (전체 p_i의 합 = 1)
이를 이항분포의 관점에서 나타내보자면 다음과 같다.

여기에서 각각 X1, X2, ... , Xk는 B(n,p_k)인 이항분포로 생각할 수 있다.
이를 통해 다항분포의 확률질량함수를 아래와 같이 구할 수 있다.
이 때 x들의 합은 n이 되고, p들의 합은 1이 된다.

ex) 멘델의 유전법칙에서 독립법칙의 예시로 완두의 껍질모양(R,r)과 색(Y,y)이 독립적으로 발현된다고 한다.
이 때 유전자형이 RRYY인 완두와 rryy인 완두를 자기수분시키면 발현비율이 RY:Ry:rY:ry=9:3:3:1로 나온다.
그렇다면 독립적으로 n개의 자기수분된 완두를 얻었을 때 (RY,Ry,rY,ry)에 속한 완두 수를 (X1,X2,X3,X4)라고 하면 확률질량함수는 다음과 같다.

이러한 다항분포에서 특정 결과에만 관심을 가지는 경우가 있을 것이다.
예를 들어, i번째 결과에만 관심이 있을 경우, 나머지 결과를 하나로 묶어 X_i~B(n,pi)인 이항분포로 표현할 수 있다.
또한, i번째 또는 j번째 결과에 관심이 있을 경우 Y=Xi+Xj로 두면 B(n,pi+pj)로 구할 수 있다.
이 때 기댓값과 분산은 이항분포에서 구하던 방식대로 구하면 된다.

이제 Xi와 Xj가 서로 어떤 관계를 가지고 있는지 공분산을 구해보고자 한다.
이 때 과정을 단순하게 만들기 위해 n=2라고 가정하고 풀면 다음과 같다.

이를 통해 Xi와 Xj의 상관계수를 구하면 아래와 같이 된다.
여기에 등장한 성공확률/실패확률인 오즈(odd)는 통계학에서 중요하게 많이 쓰이므로 기억해두는 것이 좋다.
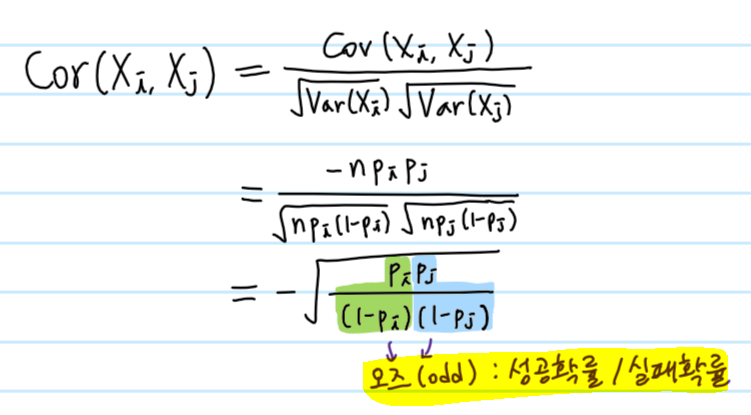
또한 분산에 대해 계산하면 다음과 같은 식이 나오게 된다.

ex) 멘델의 유전법칙
case 1] 독립법칙의 예시였던 완두의 껍질모양(R,r)에만 관심을 가지고 있다고 하자.
그러면 R:r=12:4=3:1이 되고 R의 개수 Y=X1+X2~B(n,0.75)가 된다.
case 2] 100개의 완두 중 우성인자만 있는 것과 열성인자만 있는 완두의 상관계수는?
p1=9/16, p2=1/16 --> Cov(X1,X4) = -100*9/16*1/16, Cor(X1,X4) = -sqrt( (9/16*1/16) / (7/16*15/16) )
다항분포에서 알아두면 좋을 상관관계 특징
다항분포에서 두 확률변수의 상관관계를 구할 때,
둘 다 큰 확률(p)을 가지고 있다면 상대적으로 큰 음의 상관관계를 가진다.
'MATH & STATS > STATISTICS' 카테고리의 다른 글
| [통계학] 11-2. 정규분포 - 정규분포의 성질 (0) | 2020.03.10 |
|---|---|
| [통계학] 11-1. 정규분포 - 정규분포와 확률계산 (0) | 2020.03.10 |
| [통계학] 10-2-2. 주요 이산확률분포 - 음이항분포 (0) | 2020.03.10 |
| [통계학] 10-2-1. 주요 이산확률분포 - 기하분포 (0) | 2020.03.09 |
| [통계학] 10-1. 주요 이산확률분포 - 포아송분포 (0) | 2020.03.09 |



