[통계학] 10-2-2. 주요 이산확률분포 - 음이항분포

이 포스트는 K-MOOC 숙명여대 여인권 교수님의 통계학의 이해 Ⅰ 강의를 기반으로 작성되었습니다.

이번에는 베르누이 실행의 또 다른 응용 형태인 음이항분포에 대해 알아보고자 한다.

음이항분포 (Negative Binomial Distribution)

성공할 확률이 p인 베르누이 시행을 r번 성공할 때까지 시행하는 경우 실패횟수(또는 시행횟수)의 분포
먼저 시행횟수를 기준으로 설명해보자. 실패횟수 X에 r을 더하면 시행횟수 Y(=X+r)가 되는데 이는 y-1번째까진 r-1번의 성공과 y-r번의 실패가 있었다는 것이다. Y~NB(r,p)로 나타내며, 확률질량함수는 아래와 같다.

시행횟수 기준 음이항분포

이제 실패횟수를 기준으로 설명해보자면, r번 성공할 때까지 시행하는 것이기에 실패횟수가 x번일 때 성공횟수는 r-1번일 것이며, 총 시행횟수는 x+r-1번일 것이다. 따라서 확률질량함수는 아래와 같이 된다.

실패횟수 기준 음이항분포

ex) 5명과 차례로 가위바위보를 할 때, 이길 때까지 같은 사람과 계속 가위바위보를 하고 이기면 다음 사람으로 이동할 수 있다고 하자. 이 때 게임이 끝날 때까지 10회 이하로 가위바위보를 할 확률은?

음이항분포 예시 계산

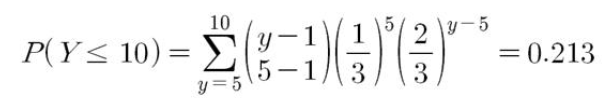
베르누이 실행을 성공할 때까지의 실패횟수 분포를 나타내는 기하분포를 r개 합하면 음이항분포가 되므로, 음이항분포의 기댓값은 기하분포를 통해 다음과 같이 구할 수 있다. 

음이항분포의 기댓값

계수자료 분석에서 표본평균과 표본분산의 차이가 심하게 날 경우, 포아송분포를 사용할 수 없으므로 음이항분포를 대체하여 사용한다.