[통계학] 3-2. 일변량 자료에 대한 수치적 기술통계 - 수치자료의 대체중심위치

이 포스트는 K-MOOC 숙명여대 여인권 교수님의 통계학의 이해 Ⅰ 강의를 기반으로 작성되었습니다.

• 표본중앙값 (sample median, 표본중위수)
  자료를 크기 순서로 나열했을 때 중앙에 있는 값
  순서통계량(order statistics) : 표본을 오름차순으로 정렬한 것

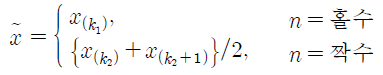
• 표본절사평균 (sample trimmed mean)
  robust하지 않은 평균의 단점과 자료의 정보를 다 활용하지 못하는 중앙값의 단점을 보완
  순서통계량에서 하위 α%까지의 자료를 이용하여 표본평균 계산
  α백분위수 : 하위 α%에 해당하는 값
  (α = 0 : 표본평균 / α = 50 : 표본중앙값)
  실제 사용하는 데이터 수 : n-2k (k=상위/하위 α%에 해당하는 데이터 수)
  ex) 체조, 피겨스케이팅 등 채점

• 표본최빈값 (sample mode)
  자료 중 빈도가 가장 많은 값을 중심 위치로 사용
  단점) 최빈값이 여러개 나올 수도 있고, 없을수도 있음(연속 자료)

히스토그램에서 최빈값 구하는 방법